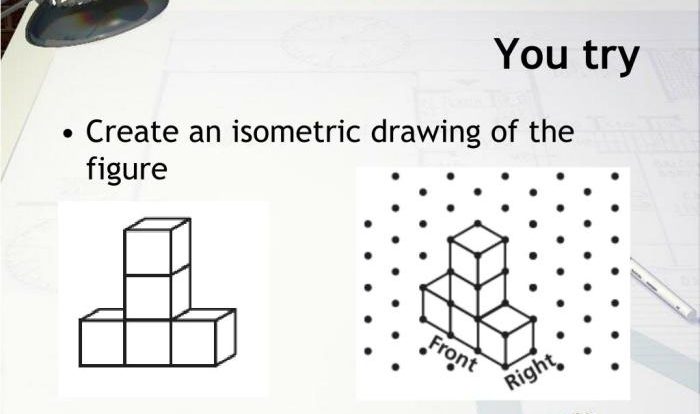
Geometry review packet #1 gina wilson – Geometry Review Packet #1 by Gina Wilson is an invaluable resource for students seeking to deepen their understanding of geometry. This comprehensive guidebook provides a thorough exploration of fundamental concepts, measurements, transformations, constructions, coordinate geometry, and geometric proofs, equipping learners with the knowledge and skills necessary to excel in this captivating field.
Through engaging explanations, illustrative examples, and practice problems, this review packet fosters a solid foundation in geometry. It serves as an ideal companion for classroom instruction, offering additional support and reinforcement for students to grasp complex geometric principles and their practical applications.
Geometry Concepts
Geometry is a branch of mathematics that deals with the properties and relationships of shapes, sizes, and spatial relationships.
Some fundamental concepts in geometry include:
Points
- A point is a location in space that has no size or shape.
- Points are often represented by dots.
Lines
- A line is a straight path that extends infinitely in both directions.
- Lines are often represented by arrows.
Planes
- A plane is a flat, two-dimensional surface that extends infinitely in all directions.
- Planes are often represented by grids.
Angles
- An angle is formed by two rays that share a common endpoint.
- Angles are measured in degrees.
Geometric Shapes
- Geometric shapes are figures that have specific properties, such as the number of sides, angles, and vertices.
- Some common geometric shapes include triangles, squares, circles, and cubes.
Geometric Measurements
Geometric measurements are essential for understanding the properties and relationships of geometric shapes. These measurements include area, perimeter, and volume, and are used in a wide range of applications, from architecture to engineering to everyday life.
Area
The area of a geometric shape is a measure of the surface enclosed by the shape. For example, the area of a rectangle is calculated by multiplying its length by its width, while the area of a circle is calculated by multiplying the square of its radius by pi (π).
- Rectangle: A = l × w
- Triangle: A = (1/2) × b × h
- Circle: A = πr²
Perimeter
The perimeter of a geometric shape is the total distance around the shape. For example, the perimeter of a rectangle is calculated by adding the lengths of all four sides, while the perimeter of a circle is calculated by multiplying its diameter by pi (π).
- Rectangle: P = 2l + 2w
- Triangle: P = a + b + c
- Circle: P = πd
Volume
The volume of a geometric shape is a measure of the space enclosed by the shape. For example, the volume of a rectangular prism is calculated by multiplying its length, width, and height, while the volume of a sphere is calculated by multiplying (4/3)π by the cube of its radius.
- Rectangular prism: V = l × w × h
- Sphere: V = (4/3)πr³
Geometric Transformations

Geometric transformations are operations that move, flip, or turn geometric shapes in a plane or space. They preserve the size and shape of the original figure, but change its position or orientation.
The three main types of geometric transformations are translations, rotations, and reflections.
Translations, Geometry review packet #1 gina wilson
A translation moves a shape from one point to another without changing its size or orientation. The distance and direction of the movement are specified by a vector.
For example, if a shape is translated 5 units to the right, each point of the shape moves 5 units to the right.
Rotations
A rotation turns a shape around a fixed point called the center of rotation. The angle of rotation is measured in degrees.
For example, if a shape is rotated 90 degrees clockwise around its center, each point of the shape moves 90 degrees clockwise around the center.
Reflections
A reflection flips a shape over a line called the line of reflection. The line of reflection is perpendicular to the plane of the shape.
For example, if a shape is reflected over the y-axis, each point of the shape is flipped over the y-axis.
| Transformation | Effect |
|---|---|
| Translation | Moves a shape from one point to another without changing its size or orientation. |
| Rotation | Turns a shape around a fixed point called the center of rotation. |
| Reflection | Flips a shape over a line called the line of reflection. |
Geometric Constructions

Geometric constructions involve using a compass and straightedge to create geometric shapes with specific properties. These constructions are fundamental in geometry and have practical applications in various fields.
The basic steps involved in geometric constructions are:
- Draw the given segments and angles.
- Use the compass to construct circles and arcs.
- Use the straightedge to draw lines and rays.
- Measure and transfer distances and angles.
Some common geometric constructions include:
- Constructing a perpendicular bisector of a line segment
- Constructing an angle bisector
- Constructing a parallel line
- Constructing a triangle given its side lengths or angles
- Constructing a circle given its center and radius
Geometric constructions are used in various applications, such as:
- Architecture and engineering
- Design and manufacturing
- Surveying and navigation
- Art and graphics
Coordinate Geometry

Coordinate geometry, also known as analytic geometry, is a branch of mathematics that uses algebra to study geometry. It is based on the idea of representing points in a plane or in space using numbers called coordinates.
The coordinate plane is a two-dimensional plane that is divided into four quadrants by two perpendicular lines, the x-axis and the y-axis. Each point in the coordinate plane is identified by an ordered pair of numbers (x, y), where x is the distance from the point to the y-axis and y is the distance from the point to the x-axis.
Distance Formula
The distance formula is a formula that calculates the distance between two points in the coordinate plane. The distance formula is given by:
d = √((x2
- x1)² + (y2
- y1)²)
where (x1, y1) and (x2, y2) are the coordinates of the two points.
The distance formula has many applications in geometry, such as finding the length of a line segment, the area of a triangle, and the volume of a sphere.
Geometric Proofs: Geometry Review Packet #1 Gina Wilson
Geometric proofs are logical arguments that establish the truth of geometric statements, known as theorems. They are essential for building a solid foundation in geometry and developing critical thinking skills.
There are two main methods of geometric proofs: synthetic proofs and analytic proofs. Synthetic proofs use axioms, postulates, and previously proven theorems to deduce new theorems. Analytic proofs use algebraic equations and coordinate geometry to prove geometric properties.
Types of Geometric Proofs
- Direct Proofs:Prove a statement is true by providing a logical sequence of steps that leads to the desired conclusion.
- Indirect Proofs:Assume the statement is false and show that this leads to a contradiction, thereby proving the statement is true.
- Proof by Contradiction:A specific type of indirect proof where the assumption leads to a statement that is known to be false.
- Proof by Cases:Divide the problem into different cases and prove the statement for each case.
Importance of Geometric Proofs
- Develop logical reasoning and problem-solving skills.
- Verify and validate geometric theorems and properties.
- Build a strong foundation for more advanced mathematics, such as calculus and trigonometry.
- Enhance spatial reasoning and visualization abilities.
FAQ Corner
What topics are covered in Geometry Review Packet #1 by Gina Wilson?
Geometry Review Packet #1 covers fundamental geometry concepts, measurements, transformations, constructions, coordinate geometry, and geometric proofs.
Is Geometry Review Packet #1 suitable for students of all levels?
This review packet is designed to support students at various levels, providing a comprehensive review of geometry concepts and their applications.
How can I access Geometry Review Packet #1 by Gina Wilson?
Geometry Review Packet #1 is typically available through online platforms or educational institutions that utilize Gina Wilson’s geometry resources.